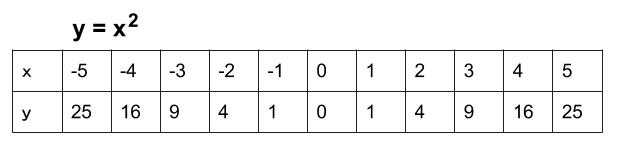
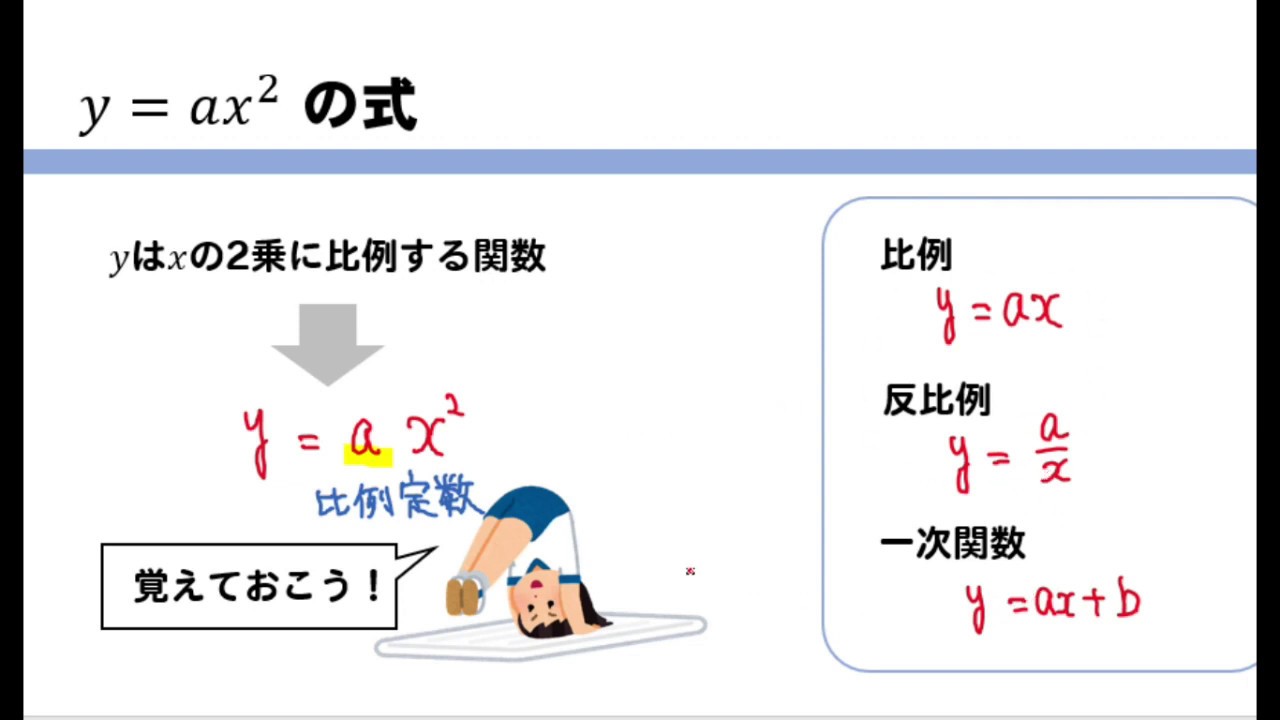
Yax二乗のグラフ
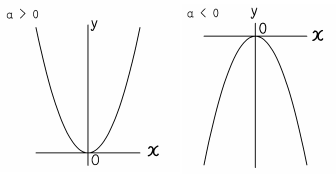
2乗に比例する関数 グラフ

関数y Ax2乗の変域の求め方 勉強ナビゲーター
授業実践記録
中学数学 関数
Q Tbn 3aand9gcru2iplpx7jxpf7sz6ft51ojwmahbxzx54u6zt1navzyfq6nd P Usqp Cau

例題で学ぶ高校数学 Y Ax2
この記事ではこんなことを書いています 最小二乗法によってデータの回帰直線を求める方法を丁寧に解説していきます。 まずは、最小二乗法とは何かということを数式を使わずにざっくりと理解します。 その後、最小二乗法の式の導出を途中の計算式を省略せずに紹介します。 最後に、その.

Yax二乗のグラフ. できたグラフがこちら。 いい感じの直線が引けました。 y = ax + b型関数への近似. 数学の問題です y=x二乗+1のグラフに、(2.1)から引いた接線があります。(傾きは2a) この式の方程式を求めるとき、途中で式が、 y-(a二乗+1)=2a(x-a)となる意味が分かりません(特にa二乗+1のところ. ・y=ax 2 +q のグラフ ↓ →例題 ↓ y=ax 2 +q のグラフ y=ax 2 +q のグラフを y=ax 2 のグラフと比較しながら考えてみます。 やはり表を作ってみることが大切です。 下の表は 2x 2 と 2x 2 +1 を比較したものです。 xのどの値においても, 2x 2 +1 の値は 2x 2 の値に1を足したものです。 したがって, y=2x 2 +1 の.
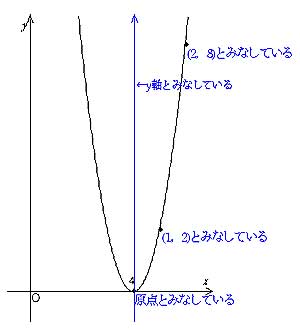
A(2,1), B(2,8) A(4, -4), B(4, -8) A(-3, 1), (-3, -9) 図の放物線lはy= 1 2 x 2 の グラフで、放物線mはy=ax 2 のグラフである。lとmがx軸に平行な直線nと交わる点をそれぞれA, Bとする。Aのx座標が4. 今日は二次関数y = ax2 のグラフをかくんだ! どちらかというと、今日は「絵を描く」感覚(^_-)-☆. 関数 y=ax 2 のグラフ(3) 関数 y=ax 2 のグラフ(4) 変域とグラフ(1) 変域とグラフ(2) 変域の割合(1) 変域の割合(2) 変域の割合(3).
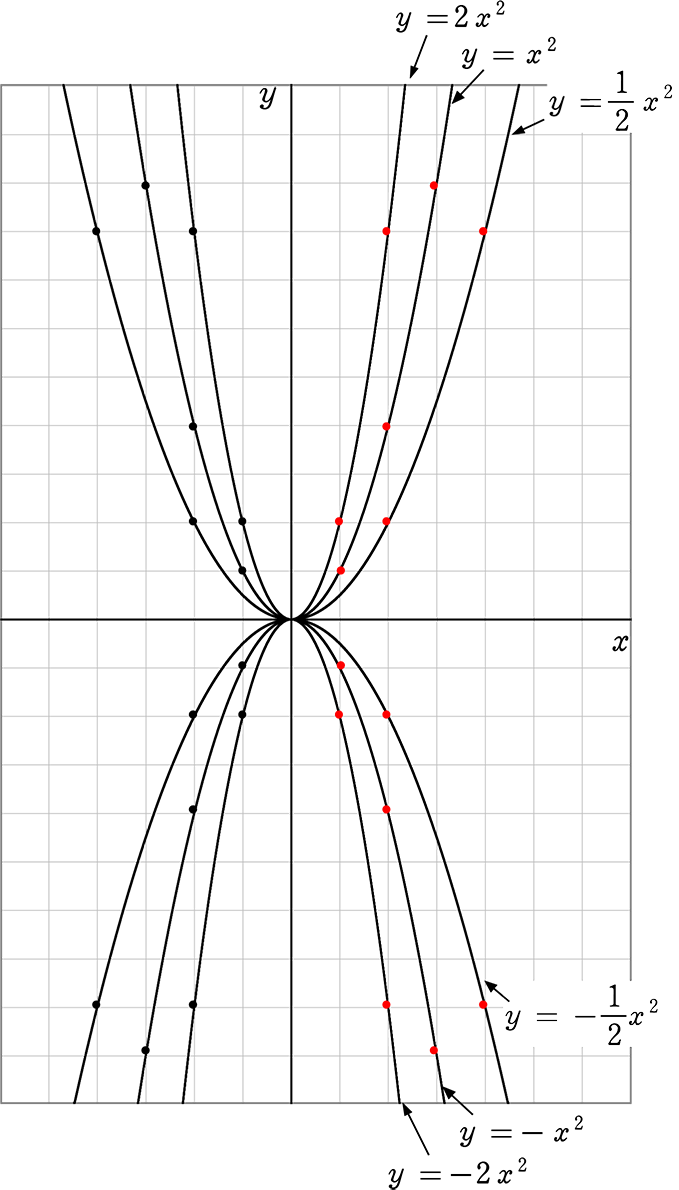
数y=ax2としてとら えられる2つの数量 を見いだし、式で表 そうとしている。 2 ・関数y=ax2 関数y=ax2の関係 を、表や式に表す ことができる。 1組のx,yの値 から関数y=ax2の 式を求めることが できる。 関数y=ax2の意味 や特徴を理解して いる。 数2. 2乗に比例する関数のグラフの特徴の問題です基本のポイント 必ず原点を通り、その原点が頂点である y軸について対称である a > 0のときは上に開き、a < 0のときは下に開く aの絶対値が小さいほどグラフの開きが大きい y=ax2のグラフとy=-ax2のグラフはx軸について対象である。. ・関数y=ax2の変化の割 合を求めることができる。 ・関数y=ax2の表,式, グラフを用いて,具体的な 事象を表現することがで きる。 ・関数y=ax2の意味を理 解している。 ・関数y=ax2のグラフや 変化の割合などの特徴を 理解している。.
2次関数 y=2x 2 −12x+19 のグラフを x 軸の正の向きに 2 , y 軸の正の向きに 3 だけ平行移動してできるグラフの方程式は次のうちどれか. 1. y=2x 2 −12x−2 2. y=2x 2 −4x+5 3. y=2x 2 −x+54 4. y=2x 2 −14x+22 5. y=−2x 2 −4x+5 2次関数のグラフの平行移動. 初等解析学において、不定元 x に関する高々一次の多項式 ax + b ( a, b は実 定数)に対し、 x を実変数とみて得られる写像 ,:. が必要だったじゃん?? 一次関数の式は「y=ax +b」で未知数がaとbの2つあったからね。 それとくらべると、.
数学 関数y=ax二乗グラフと四角形の問題です。 答えしか乗っていなくて、解き方が分からないので教えて頂けるとありがたいです。 答えは①が4,②がa=三分の一です。宜しくお願い致します。. 関数y=ax2の関 係などを,表,式,グ ラフを用いて的確に表 現したり,数学的に処 理したりするなど,技 能を身に付けている。 事象の中には関数y =ax2などとして捉 えられるものがあるこ とや関数y=ax2の 表,式,グラフの関連. ↦, = + を一次函数と呼ぶ(見かけ上一次なだけでなく実際に「一次」であることを要請する場合は「 a ≠ 0 」とする)。 )。定数函数となる a = 0.
また,関数y=ax 2 はy軸を対称の軸にして左右対称ですので,-2と4で,xの絶対値が大きい方がyの最大値をとることも考えましょう。 試しにx=-2とx=4の両方を代入してみましょう。x=-2のときはy=4a,x=4のときはy=16aになりますね。. さくなるように、係数を決める方法である。以下に測定値から最適な直線y = ax+bの係数a とbを決定する手順を示す。 S = X (yi −axi −b)2 (残差の二乗和) ∂S ∂a = 2 X xi(axi +b−yi) = 2 X (ax2 i +bxi −xiyi) = 0 ∂S ∂b = 2 X (axi +b−yi) = 0 これらより、下記の連立方程式. 関数y=ax2 (a>0)のグ ラフをかくこ とができる。 (学習活動の観 察、ノートの分 析) y=ax2 のa>0 のときのa の 値とグラフの 関係を理解し ている。(学習 活動の観察、発 表の様子) 5 関数y=ax2 のグラフ (2) 関数y=ax 2のグラフ は、a の符号によってど の.
求める直線の方程式をy=ax+bとします。このときaの値は a=yの増加量÷xの増加量 で求めることができます。(ここがわからない場合は、変化の割合を復習してみましょう) yの増加量=4-2=2 xの増加量=2-1=1. Y=ax 2 のグラフを,x 軸方向へ p,y 軸方向へ q だけ平行移動する。 そこで,X=x+p,Y=y+q とおくと,x=X-p,y=Y-q となるので,与式へ代入すると,Y-q=a(X-p) 2. まず、一次関数とは、y = ax + b という式で表されるものです。 これをエクセル上で表し、グラフにしていきましょう。今回はy=5x+2という一次方程式を描いていきましょう。 まずは、xの値を1刻みで入力していきます。 続いて、一次関数のyの値を求めていき.
4 関数y=ax2 のグラフと変域(1) VMA-05 3 2 乗に比例する関数の増加・減少 ここでは,関数y=ax2 の値の増加・減少について学習してみましょう。 関数y=ax2 でxの変域が与えられたときのyの最大値・最小値は,たとえばa>0 のとき のように, xの変域によって考え方が違ってきます。. この生徒は,xの値をn倍すれば,yの値はn 2 倍になるという二乗に比例する関数の表における性質を活用して説明した。また,実際に走る場面では速度には限界があり一定の値になることから比例のグラフになると予想し. 基本二次関数y=ax^2+qのグラフ 基本二次関数y=a(x-p)^2のグラフ 基本二次関数y=a(x-p)^2+qのグラフ 標準二次関数y=ax^2+bx+cのグラフ(具体例) 標準平方完成のやり方 標準二次関数y=ax^2+bx+cのグラフの頂点.
イ 関数y=ax2 について,表,式,グラフを相互に関連付けて理解すること。 ウ 関数y=ax 2 を用いて具体的な事象をとらえ説明すること。 エ いろいろな事象の中に,関数関係があることを理解すること。. Xとyを代入しちまえば、aしか残らないってわけ。 解き方も簡単でうれしいね。 中学2年生でならった一次関数のときは、 グラフが通る2つの座標. これが 両対数グラフにすると直線になるカラクリ です。 つまり、「 もともとの\(x\)と\(y\)の関係性がべき関数を使った(\(y=ax^{-b}\))の関係性があるから両対数グラフにすると直線になる 」のです。 まとめ.
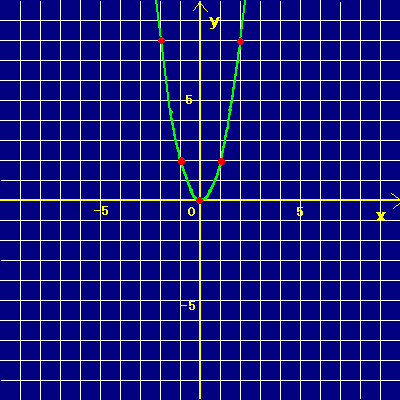
この映像授業では「中3 数学 関数y=ax^2③ グラフ1」が約13分で学べます。問題を解くポイントは「y=ax^2のグラフは、原点を通る放物線」です。. Y=ax 2 (a>0)のグラフは、図のように 「原点を通る、上に開いた放物線」 になるよ。 U字型 のイメージだね。 例題をいっしょに解きながら、実際にグラフが 「原点を通る、上に開いた放物線」 になることを確認していこう。. 基本二次関数y=ax^2+qのグラフ 基本二次関数y=a(x-p)^2のグラフ 基本二次関数y=a(x-p)^2+qのグラフ 標準二次関数y=ax^2+bx+cのグラフ(具体例) 標準平方完成のやり方 標準二次関数y=ax^2+bx+cのグラフの頂点.
二次関数y=ax二乗でグラフは(4.2)を通っているy軸上に点ビーをab = ob (oは原点)となるようにとるこの時bのY座標を求めるにはどうしたらいいのですか?お願いします全然わからんです問題文を、1文字1文字(句点や読点を含む)の全. すなわち直線の式が y=ax+b となるようにa,bを求めます。 falseを指定すると、y切片が0になるように、すなわち直線の式が y=ax となるようにaを求めます。 出力について y切片の値が0と指定、すなわち =linest(c5:c10,b5:b10,false).

2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ

高校数学 Y Ax 2 Bx Cのグラフ 例題編 映像授業のtry It トライイット

関数y Ax2乗の変域の求め方 勉強ナビゲーター
中3数学 関数y ax二乗 放物線と直線1 発展問題 問題 324 プリント

中学数学 二次関数y Ax2のグラフから式を3秒で読み取る方法 Qikeru 学びを楽しくわかりやすく
中3 2次関数

Q Tbn 3aand9gcr3u7a3jgkomdi6kdfbd7atd95s1xtjfc1beg Usqp Cau
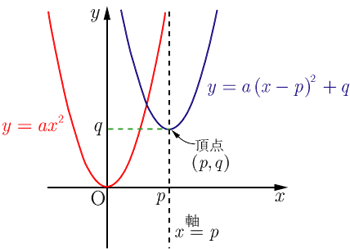
2次関数のグラフ Y A X 2 P Q

Y Ax2乗 Aの求め方についてパターン別に解説 発展問題もアリ 中学数学 理科の学習まとめサイト

2次関数のグラフと直線
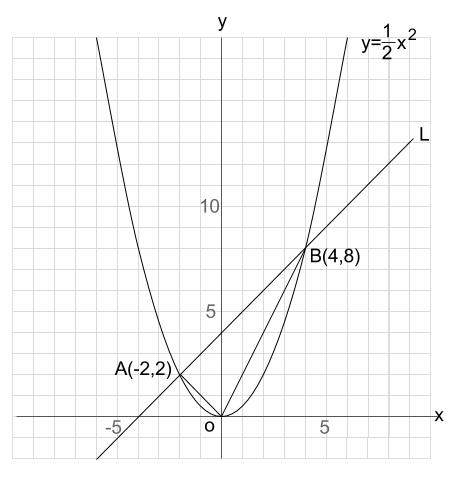
中学数学 Y Ax 2 図形との融合問題 中学数学の無料オンライン学習サイトchu Su

2次関数 Y A X P のグラフの書き方 グラフの平行移動 数学i By ふぇるまー マナペディア

中3数学 Y Ax 2の増減 映像授業のtry It トライイット

高校数学 Y Ax 2のグラフ 下に凸 上に凸 映像授業のtry It トライイット

2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ

関数y X 2のグラフの性質 勉強ナビゲーター
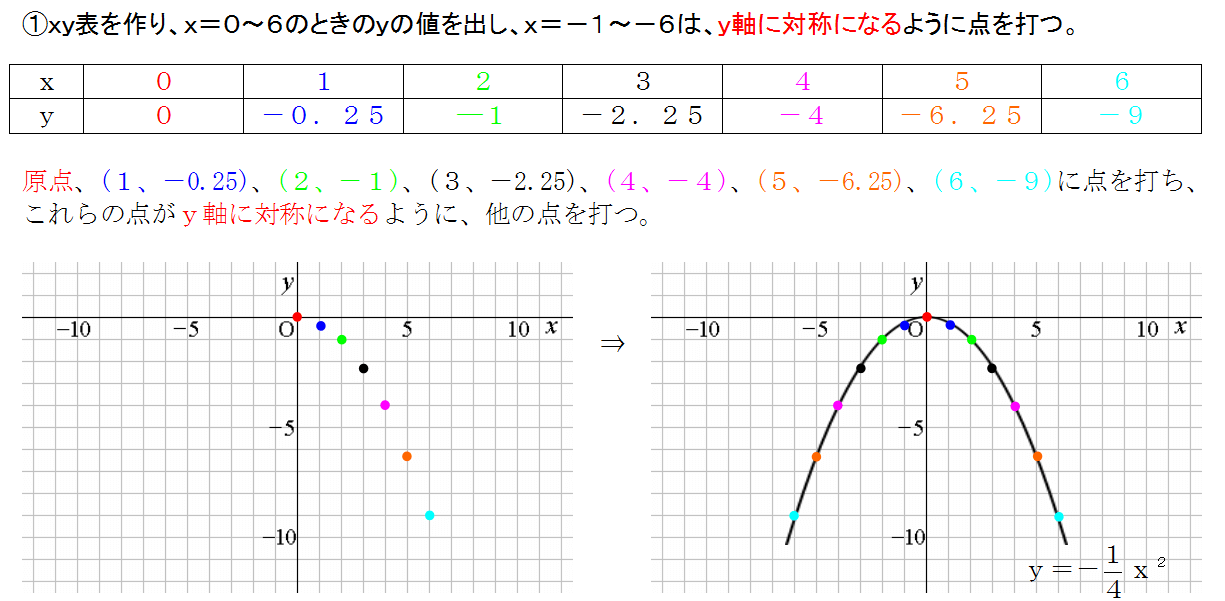
二次関数のグラフの書き方 中学生の数学で非常に大切だ 三重の個人契約家庭教師
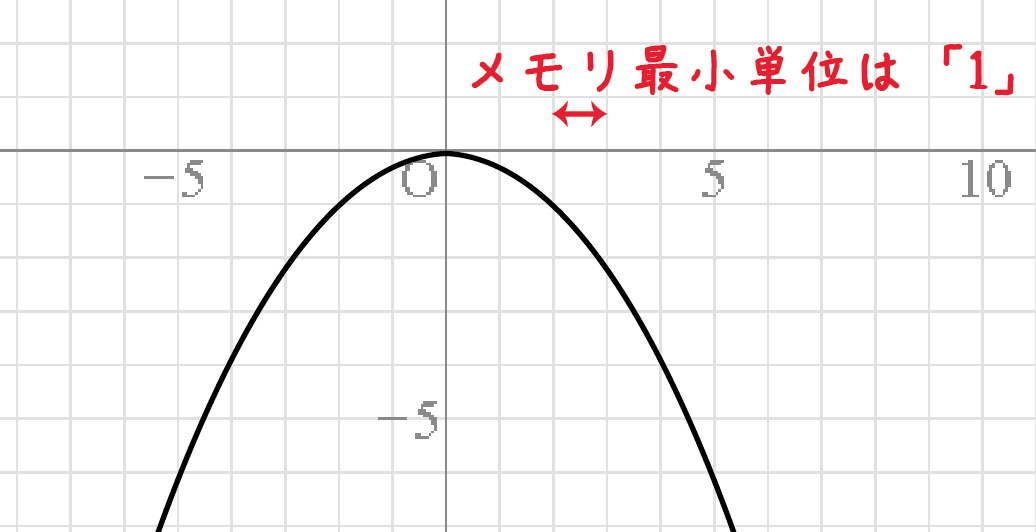
中学数学 二次関数y Ax2のグラフから式を3秒で読み取る方法 Qikeru 学びを楽しくわかりやすく

基本 二次関数y A X P 2のグラフ なかけんの数学ノート
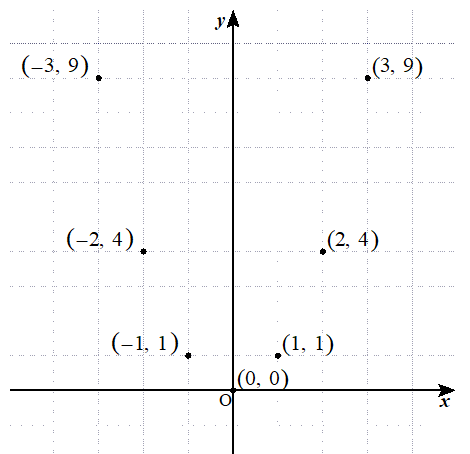
関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ

数学 関数y Ax二乗グラフと四角形の問題 中学数学に関する質問 勉強質問サイト

例題で学ぶ高校数学 Y Ax2
関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ

Aは関数y Ax二乗のグラフと直線y 3分の2x 4との交点 Bは直線y 3分の2x Clear

二次関数y Axの2乗の利用問題 グラフ 中学数学に関する質問 勉強質問サイト

二次関数y ax 2 のグラフは点a 4 2 を通っている y線 数学 教えて Goo

基本 二次関数 Y Ax 2 のグラフ なかけんの数学ノート
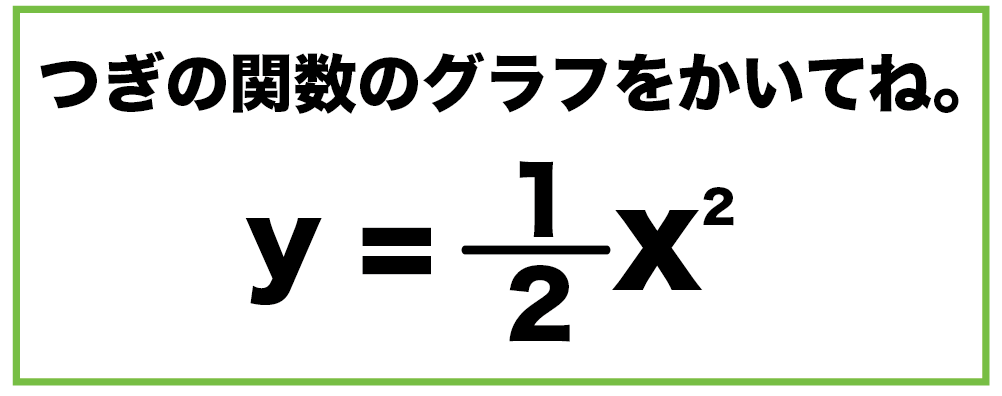
中学数学 二次関数y Ax2のグラフの書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
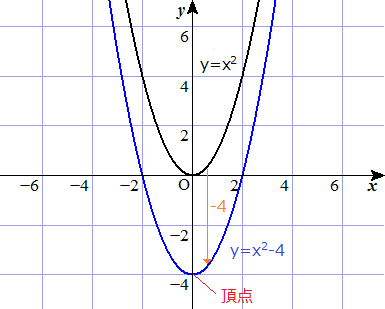
例題で学ぶ高校数学 Y Ax2 Q

関数y Ax2のグラフ まなびの学園

2乗に比例する関数のグラフ 放物線 の書き方 無料で使える中学学習プリント

中3数学 Y Ax2乗の変域の求め方を解説 数スタ

Y Axの二乗の利用問題 グラフ 中学数学に関する質問 勉強質問サイト

2乗に比例する関数のグラフ 放物線 の書き方 無料で使える中学学習プリント
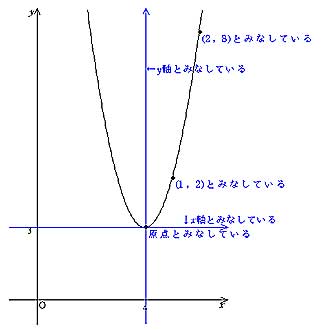
授業実践記録

Y Ax 2 Bx Cのグラフ 数学i フリー教材開発コミュニティ Ftext
Q Tbn 3aand9gctzd4cf3omkqh6au8oyyszkudxmaolx175fdsoaw2c Rrwlrg Usqp Cau

例題で学ぶ高校数学 Y A X P 2
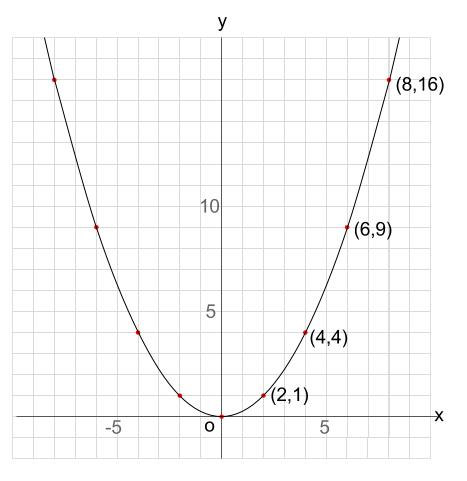
中学数学 Y Ax 2 のグラフを読み取る 中学数学の無料オンライン学習サイトchu Su
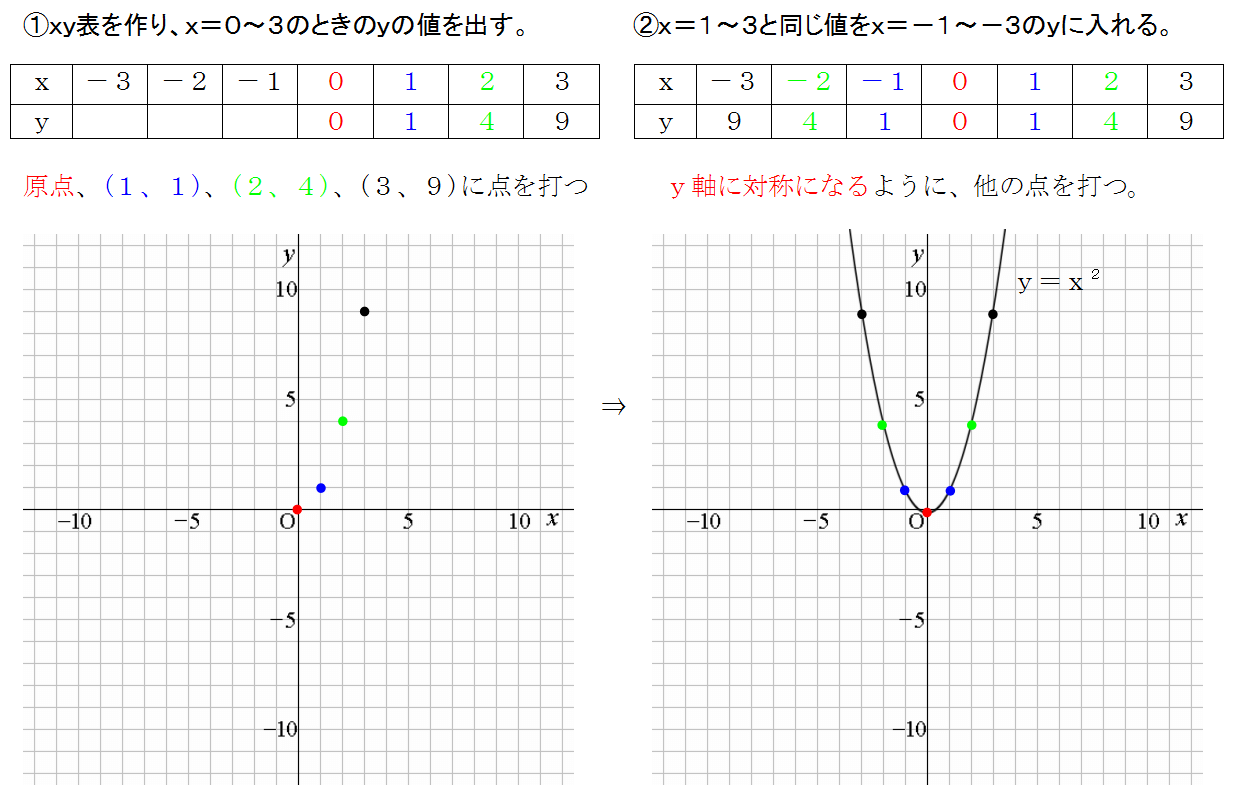
二次関数のグラフの書き方 中学生の数学で非常に大切だ 三重の個人契約家庭教師

2次関数 変域 変域からの式の決定 基 標 数学の解説と練習問題
Q Tbn 3aand9gcrafj3 Fn12sv Ue4ag4rcxujtlzubrqz0a6qeud40ix Zzrsxf Usqp Cau

Y Ax 2 Cのグラフ 数学i フリー教材開発コミュニティ Ftext
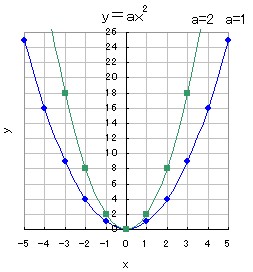
2乗に比例するグラフ 中学から数学だいすき

数 2次関数 Y Ax 2 Bx C の符号判定 高校生 数学のノート Clear
Q Tbn 3aand9gcr Z5vxxaejhlbdezscunx3z2ggtlwxlfen2qvoc6400rbbdlhi Usqp Cau
2乗に比例する関数 グラフ

Q Tbn 3aand9gctptlje5tljglpsgvaq48s Hq35eoktvrywbg Usqp Cau

中学数学 1次関数と2次関数y Ax2のグラフの3つの違い Qikeru 学びを楽しくわかりやすく
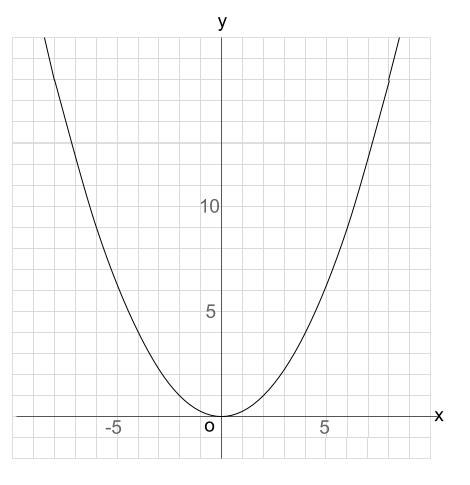
中学数学 Y Ax 2 のグラフを読み取る 中学数学の無料オンライン学習サイトchu Su
Y Ax のグラフ 中学3年 数学クラブ

Y Ax 2のグラフをexcelで作成したい Y Ax 2のグラフをexcelで作成し Excel エクセル 教えて Goo
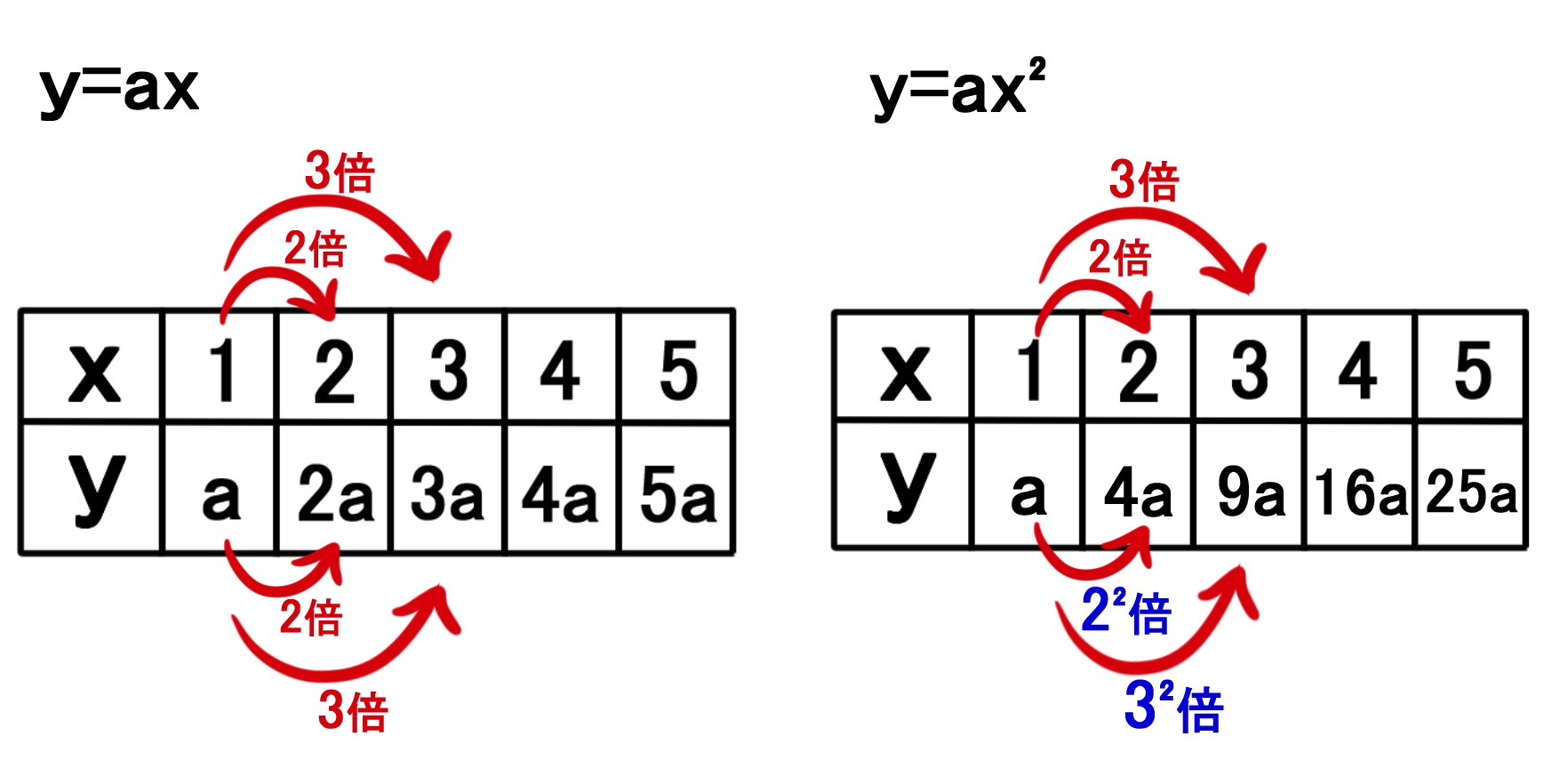
2次関数y Ax のグラフとは バカでもわかる 中学数学

中学数学 二次関数y Ax2のグラフから式を3秒で読み取る方法 Qikeru 学びを楽しくわかりやすく

例題で学ぶ高校数学 Y Ax2
中学数学 Y Ax 2 のグラフ 中学数学の無料オンライン学習サイトchu Su
関数y Ax の 変化の割合 の問題 Xの値がaからa 2まで増加したときに Yの値は バカでもわかる 中学数学
Http Www Edu City Fukuyama Hiroshima Jp Chu Johoku Revolution Actionplan Syutaiteki Manabi01 6 Shidouan K29 07m Pdf
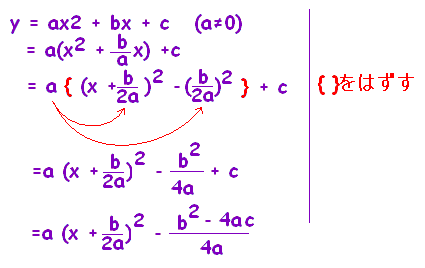
文字係数2次関数の頂点
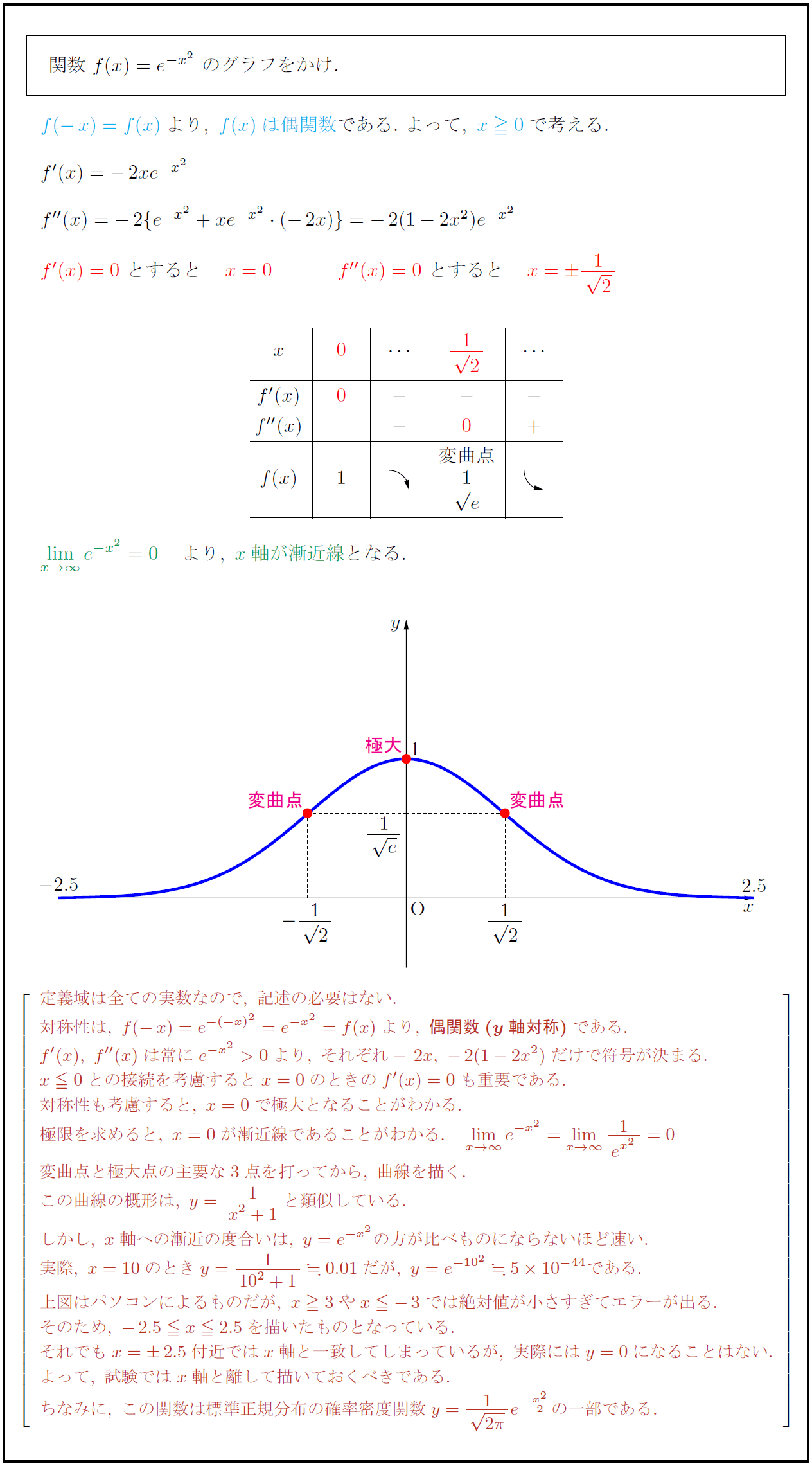
高校数学 指数関数 Y E X のグラフ 正規分布曲線もどき 受験の月

中学校数学 3年生 数量 2乗に比例する関数 Wikibooks

Y Ax 2
関数x Ax二乗のxとyの対応表の書き方を教えてください Yahoo 知恵袋
この 3 のグラフをどう書けばいいのか 誰か教えて頂けません Yahoo 知恵袋

例題で学ぶ高校数学 Y Ax2 Q

2次関数のグラフ

関数 Y Ax2 まとめ 中学生 数学のノート Clear

二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ

中学校数学 3年生 数量 2乗に比例する関数 Wikibooks
関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは Youtube
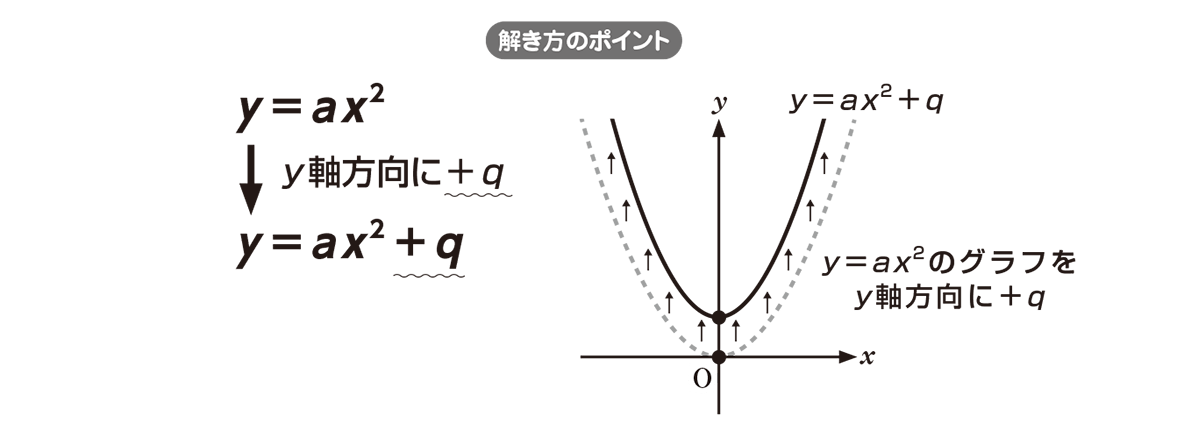
高校数学 Y Ax 2 Qのグラフ2 映像授業のtry It トライイット
関数y Ax 2では傾き 変化の割合なんですか 変化の割合 Yahoo 知恵袋

高校数学 Y Ax 2 Bx Cのグラフ 練習編 映像授業のtry It トライイット

Y Axの二乗について 中学数学に関する質問 勉強質問サイト

二次関数のグラフの問題 aの値で上か下かの向きが決まるよ 中学や高校の数学の計算問題

Y Ax 2のグラフ チーム エン

曲線 は関数y Ax二乗のグラフで直線ℓと2点abで交わっている Clear

数学 y Xの二乗の値の変化 中学生 数学のノート Clear

中学数学 二次関数y Ax2のグラフの書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

高校数学 Y Ax 2 Qのグラフ1 練習編 映像授業のtry It トライイット
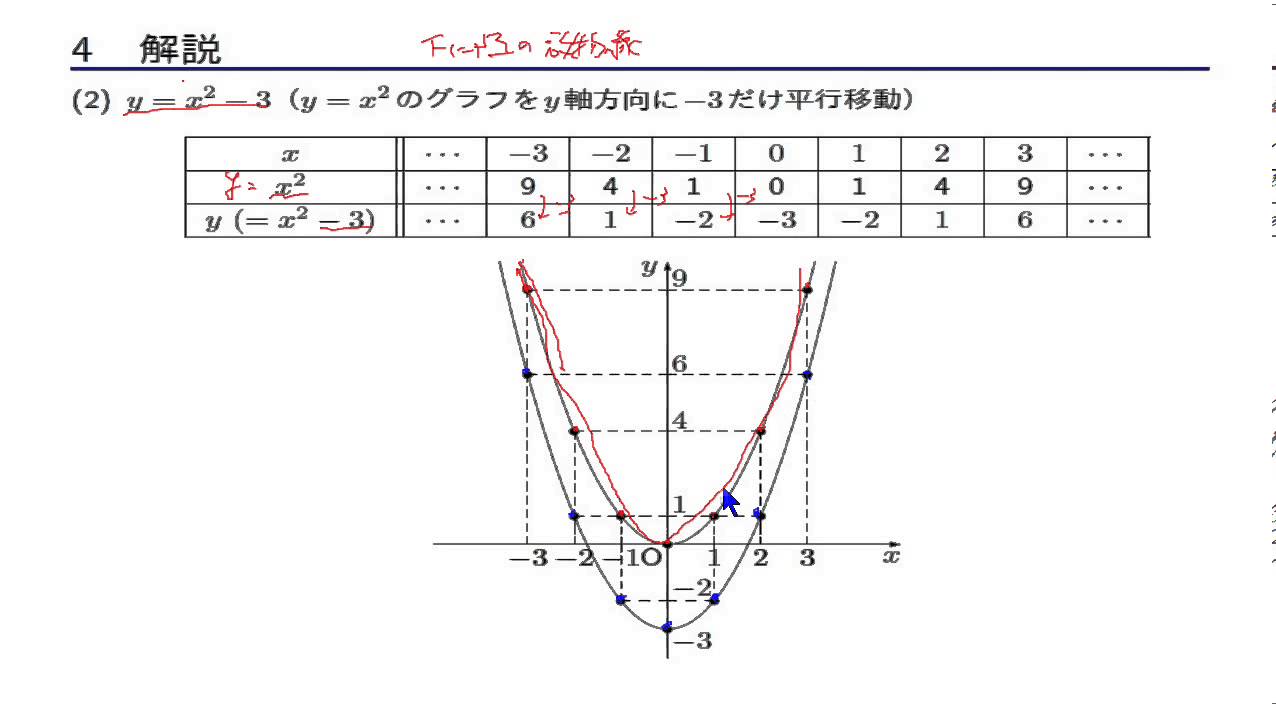
数学i 2次関数 2 2 Y Ax 2 Qのグラフ Youtube
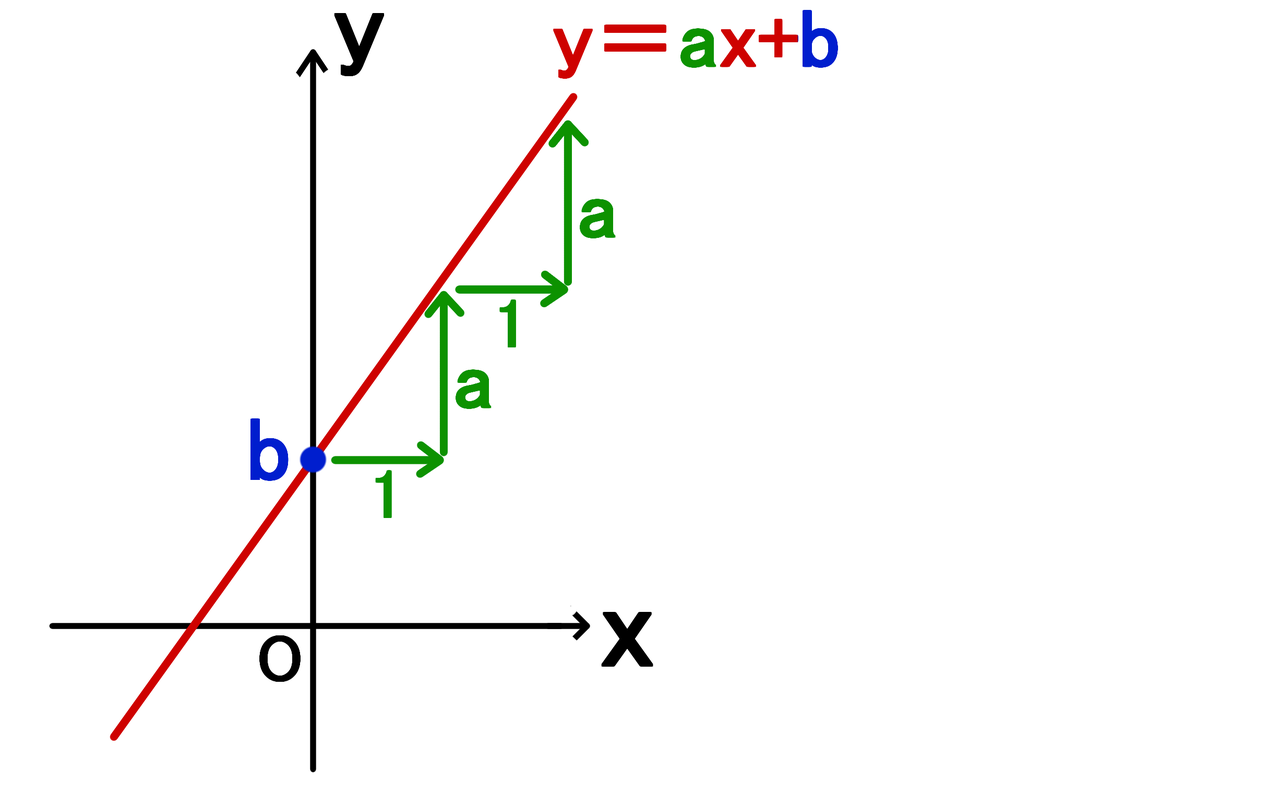
関数y Ax の 変化の割合 の問題 Xの値がaからa 2まで増加したときに Yの値は バカでもわかる 中学数学
3年 関数 Y X のグラフ 数学イメージ動画集 大日本図書
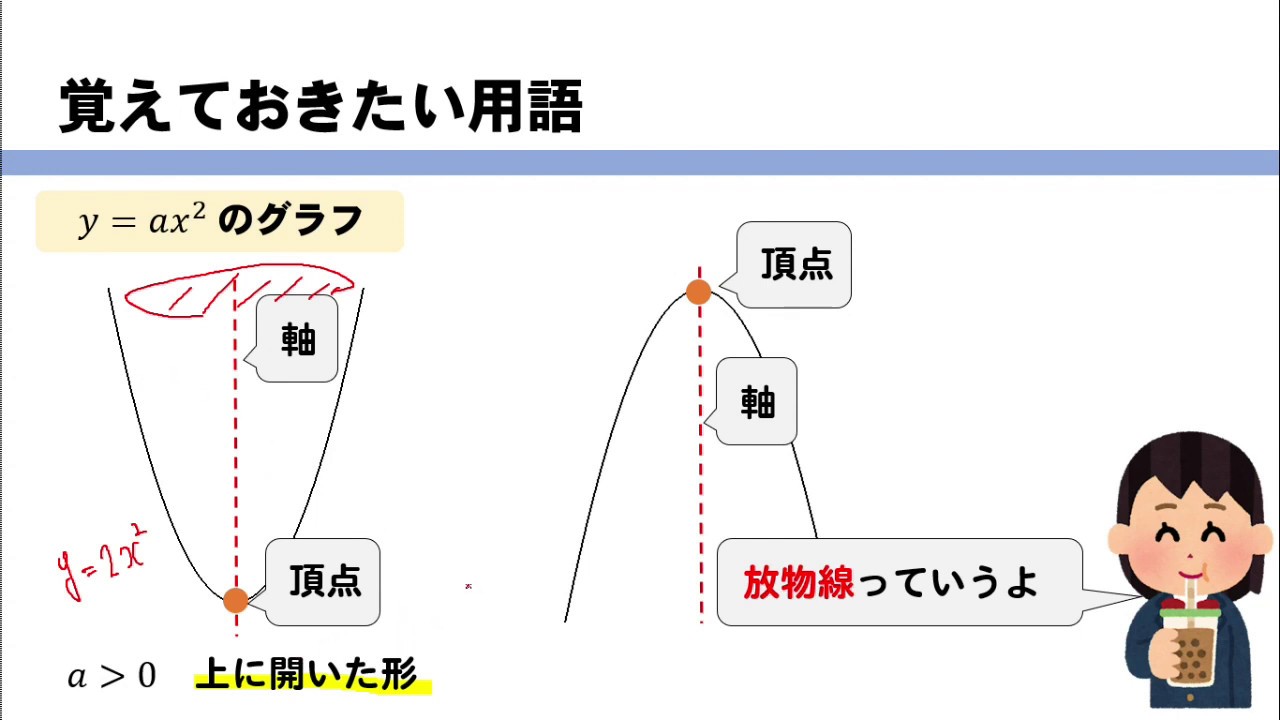
関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ

例題で学ぶ高校数学 Y Ax2 Q
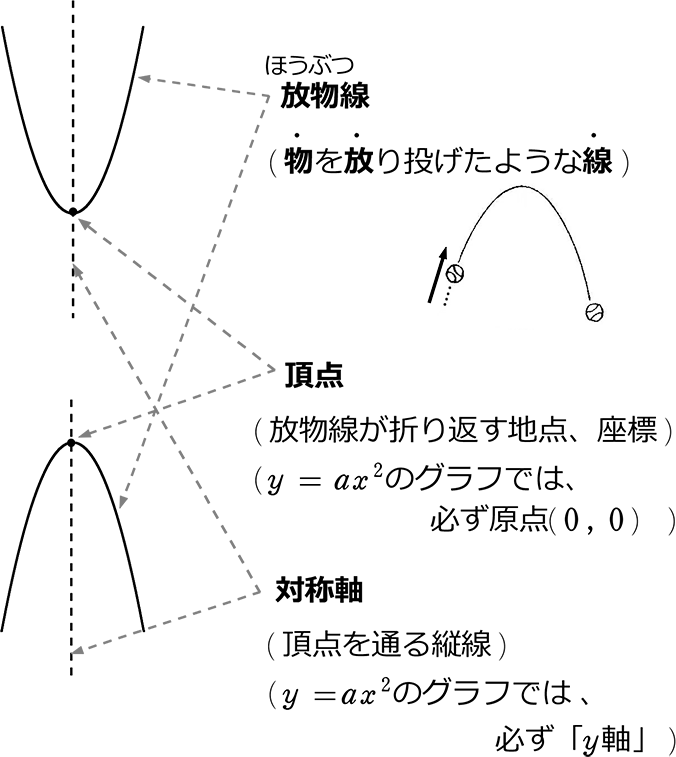
中学数学 関数

関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ
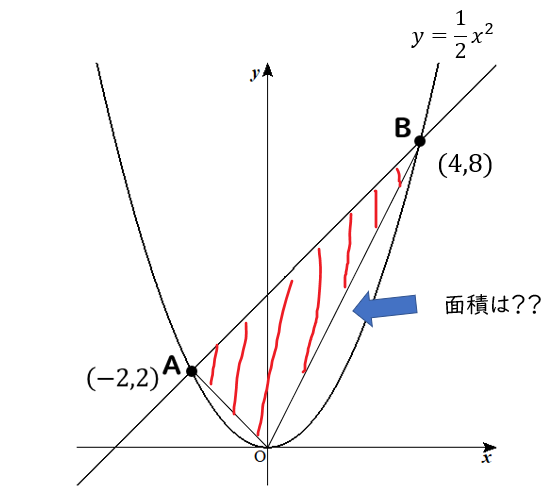
Y Ax2乗の利用 放物線と直線による面積 中学3年の問題をイチから解説 中学数学 理科の学習まとめサイト

2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ
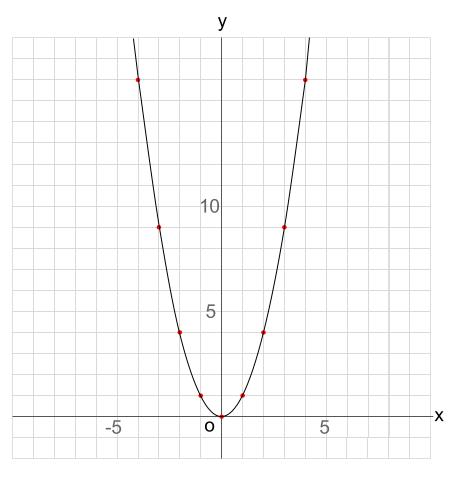
中学数学 Y Ax 2 のグラフ 中学数学の無料オンライン学習サイトchu Su

中3数学 Y Ax 2のグラフ A 0 映像授業のtry It トライイット
二次関数y Ax 2 Bx Cのグラフは 右の図のような放物線である 次の問い Yahoo 知恵袋
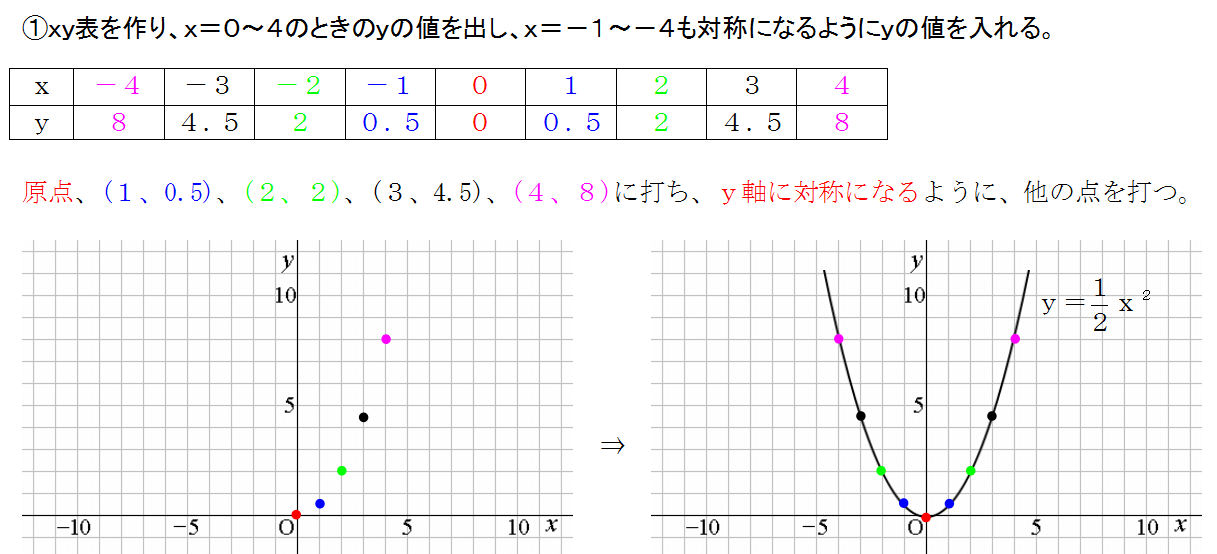
二次関数のグラフの書き方 中学生の数学で非常に大切だ 三重の個人契約家庭教師

関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ

Y Ax 2 Bx Cのグラフ 数学i フリー教材開発コミュニティ Ftext

Y Ax2乗のグラフ 中3数学 関数y Ax二乗 2 Youtube

高校数学 2次関数のグラフy Ax Bx Cの係数の符号 受験の月

二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ



